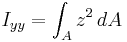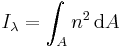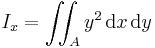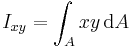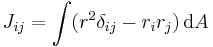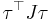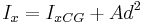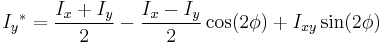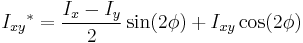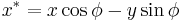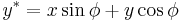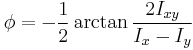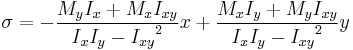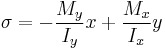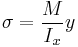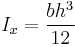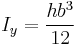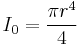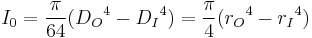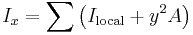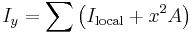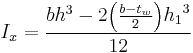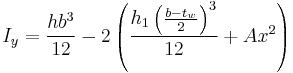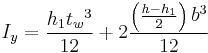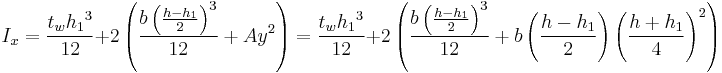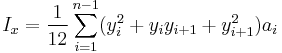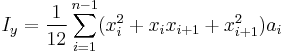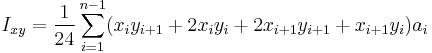Second moment of area
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane. The deflection of a beam under load depends not only on the load, but also on the geometry of the beam's cross-section. This is why beams with higher area moments of inertia, such as I-beams (properly denoted as: wide-flange beams), are so often seen in building construction as opposed to other beams with the same cross sectional area.
The second moment of area differs from polar moment of inertia of area in the direction of the axis of bending or torsion relative to the plane of the cross-section; in the latter, the axis is perpendicular to this plane. The third kind of moment of inertia not to be confused with involves angular kinetic energy or momentum. Often, each of these may simply be referred to as "moment of inertia," and the same symbols, I or J, may be used, sometimes with a qualifying subscript. Which inertia is meant (bending, twisting, or kinetic) is usually clear from the context, if not from the units: both moments of area have units of length to the fourth power [m4] (distinguished only by whether a beam is being bent or torqued), whereas the kinetic moment of inertia of mass has units of mass times length squared [kg*m2].
Contents |
Intuition
Consider the problem of determining the deflection of a beam of uniform material and uniform cross section. In particular, suppose we have a cantilevered I-beam with a weight on the end. If the beam is long, we assume the dominant deflection mode will be bending rather than shear. Thinking of the beam as made of elements along its length, like sliced bread, consider the load on one of these slices. The load will be a bending moment. Let the beam lie along the x axis with z pointing up. The bending moment would be around the y axis. The top will be in tension; the bottom will be in compression, and a horizontal line middle parallel with the y axis will experience no load. We wish to describe the effects on beam stiffness due to the cross-sectional shape of the beam as a single number (or, in the case that we want to consider more than one loading direction, as a symmetric tensor, which we can represent as a 2×2 matrix); this will be the second moment of area.
Assuming linear elasticity, the restoring stress that any point in the beam will provide, is proportional to the strain it experiences. This stress-strain relationship can be described by Hooke's law. The energy will be proportional to the square of the strain. Geometrically, the strain in the beam will be maximum at the top, decrease linearly to zero at the medial axis, and continue to decrease linearly to the bottom. Thus, the energy stored in a cross-sectional slice of the beam bent by some amount will be proportional to the sum of the square of the distance to the medial axis. In particular, the actual energy storage will also be proportional to the length of the beam and the stiffness of the material. This strain-energy storage is described well by the Minimum total potential energy principle.
Considering only the factor due to the cross-sectional shape of the beam gives the second moment of area:
Notes on notation
Some authors use Ix instead of Ixx and Iy rather than Iyy.
Definition
Let A be a beam cross section perpendicular to the beam's axis. That is, A is a plane region of a particular shape. Let λ be a straight line in the plane (by definition, perpendicular to the axis of the beam). Then the second moment of area of the region A about the line λ is
where
- Iλ = the second moment of area about the line λ
- dA = an elemental area
- n = the perpendicular distance from the line λ to the element dA
When the line λ is the x axis and the bending force is parallel to the z axis, the second moment of area can be computed as
For calculating the stresses of bending, the above can only be used on its own when sections are symmetrical about the x-axis. When this is not the case, the second moment of area about both the x- and the y-axis and the product moment of area, Ixy (see below), are required.
Product moment of area
While the scalar second moment of area about an axis describes a beam's resistance to bending along that axis, some beams will deflect in a direction other than the direction they are loaded. For example, imagine a leaf spring running along the x axis but oriented so that its surface normal is in the (0,1,1) direction. If you push down on it (0,0,−1), that will result in a bending moment in the (0,1,0) direction. However, although it will move down, it will primarily deflect in the (0,−1,−1) direction. This behavior is captured by the product moment of area. The product moment of area, Ixy is defined as
- dA = an elemental area
- x = the perpendicular distance to the element dA from the axis y
- y = the perpendicular distance to the element dA from the axis x
- Note that Ixy is defined here with positive sign following common practice adopted in structural analysis (see e.g., Pilkey 2002, p. 15).
A coordinate system in which the product moment is zero is referred to as a set of principal axes, and the second moments of area calculated with respect to the principal axes will assume their maxima and minima. This is a direct result of the spectral theorem applied to the moment tensor, described below; because it is symmetric positive semi-definite.
Second moment of area tensor
Keeping track of both second moment of area and product moment of area is confusing and tedious. A holistic approach is to note that a second moment of area is fundamentally a tensor—an object that provides deflection direction and magnitude, or elastic energy, as a function of loading direction. Much like the mass moment of inertia, the area moment of inertia tensor is
where 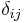 is the Kronecker delta.
is the Kronecker delta.
The reason for the 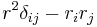 as opposed to just the outer product,
as opposed to just the outer product, 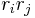 , is that the tensor operates on moments. That is, we would like the expression
, is that the tensor operates on moments. That is, we would like the expression
to be proportional to the energy for a given torque, 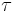 . See Moment of inertia#Comparison with covariance matrix for details.
. See Moment of inertia#Comparison with covariance matrix for details.
The product moment of area is significant for determining the bending stress in an asymmetric cross section. Unlike the second moments of area, the product moment may give both negative and positive values.
Unit
The unit for second moment of area is length to the fourth power (typically mm4, in4, etc.)
Co-ordinate transformations
When calculating moments of the section it is often practical to compute them in one co-ordinate system (typically bound to the section shape) and then transform to another one using co-ordinate transformations. As an outer product of vectors, this tensor transforms as a type (0,2) tensor.
Parallel axis theorem
The parallel axis theorem can be used to determine the moment of an object about any axis, given the moment of inertia (second moment of area) of the object about the parallel axis through the object's center of mass (or centroid) and the perpendicular distance between the axes.
- Ix = the second moment of area with respect to the x-axis
- IxCG = the second moment of area with respect to an axis parallel to x and passing through the centroid of the shape (coincides with the neutral axis)
- A = area of the shape
- d = the distance between the x-axis and the centroidal axis
Axis rotation
The following formulae can be used to calculate moments of the section in a co-ordinate system rotated relative to the original co-ordinate system:
- Ix, Iy and Ixy = the second moments and the product moment of area in the original coordinate system
- Ix*, Iy* and Ixy* = the second moments and the product moment of area in the rotated coordinate system.
The value of the angle  , which will give a product moment of zero, is equal to:
, which will give a product moment of zero, is equal to:
This angle is the angle between the axes of the original coordinate system and the principal axes of the cross section.
Stress in a beam
The general form of the classic bending formula for a beam in co-ordinate system having origin located at the neutral axis of the beam is (Pilkey 2002, p. 17):
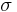 is the normal stress in the beam due to bending
is the normal stress in the beam due to bending- x = the perpendicular distance to the centroidal y-axis
- y = the perpendicular distance to the centroidal x-axis
- My = the bending moment about the y-axis
- Mx = the bending moment about the x-axis
- Ix = the second moment of area about x-axis
- Iy = the second moment of area about y-axis
- Ixy = the product moment of area
If the coordinate system is chosen to give a product moment of area equal to zero, the formula simplifies to:
If additionally the beam is only subjected to bending about one axis, the formula simplifies further:
Second moment of area for various cross sections
See list of area moments of inertia for other cross sections.
Rectangular cross section
- b = width (x-dimension),
- h = height (y-dimension)
Circular cross section
- r = radius
Hollow Cylindrical Cross Section
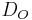 = outside diameter
= outside diameter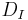 = inside diameter
= inside diameter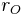 = outside radius
= outside radius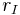 = inside radius
= inside radius
Composite cross section
When it is easier to compute the moment for an item as a combination of pieces, the second moment of area is calculated by applying the parallel axis theorem to each piece and adding the terms:
- y = distance from x-axis
- x = distance from y-axis
- A = surface area of part
- Ilocal is the second moment of area for that part of the composite, in the appropriate direction (i.e. Ix or Iy respectively).
"I-beam" cross section
The I-beam can be analyzed as either three pieces added together or as a large piece with two pieces removed from it. Either of these methods will require use of the formula for composite cross section. This section only covers doubly symmetric I-beams, meaning the shape has two planes of symmetry.
- b = width (x-dimension),
- h = height (y-dimension)
- tw = width of central webbing
- h1 = inside distance between flanges (usually referred to as hw, the height of the web)
This formula uses the method of a block with two pieces removed. (While this may not be the easiest way to do this calculation, it is instructive in demonstrating how to subtract moments).
Since the I-beam is symmetrical with respect to the y-axis the 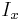 has no component for the centroid of the blocks removed being offset above or below the x axis.
has no component for the centroid of the blocks removed being offset above or below the x axis.
When computing Iy it is necessary to allow for the fact that the pieces being removed are offset from the Y axis, this results in the Ax2 term.
- A = Area contained within the middle of one of the 'C' shapes of created by two flanges and the webbing on one side of the cross section =
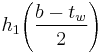
- x = distance of the centroid of the area contained in the 'C' shape from the y-axis of the beam =
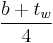
Doing the same calculation by combining three pieces, the center webbing plus identical contributions for the top and bottom piece:
Since the centroids of all three pieces are on the y-axis Iy can be computed just by adding the moments together.
However, this time the law for composition with offsets must be used for Ix because the centroids of the top and bottom are offset from the centroid of the whole I-beam.
- A = Area of the top or bottom piece =
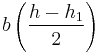
- y = offset of the centroid of the top or bottom piece from the centroid of the whole I-beam =
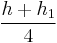
Any cross section defined as polygon
The second moments of area for any cross section defined as a simple polygon on XY plane can be computed in a generic way by summing contributions from each segment of a polygon.
For each segment defined by two consecutive points of the polygon, consider a triangle with two corners at these points and third corner at the origin of the coordinates. Integration by the area of that triangle and summing by the polygon segments yields:
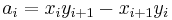 is twice the (signed) area of the elementary triangle,
is twice the (signed) area of the elementary triangle,- index i passes over all n points in the polygon, which is considered closed, i.e. point n is point 1
These formulae imply that points defining the polygon are ordered in anticlockwise manner; for clockwisely defined polygons it will give negative values. See polygon area for calculating area and centroid of the section using similar formulae.
See also
- List of area moments of inertia
- List of moments of inertia
- Moment of inertia
- Polar moment of inertia
- Parallel axis theorem
- Perpendicular axis theorem
References
- Pilkey, Walter D. (2002). Analysis and Design of Elastic Beams. John Wiley & Sons, Inc.. ISBN 0-471-38152-7.